문제항공기 모델링에서 NACA Airfoil을 활용하는 경우가 많은데, Airfoil Tools http://airfoiltools.com/ 와 같은 웹 기반의 에어포일 생성기를 사용하는 경우를 많이 보게 됩니다.
문제점1. 좌표의 노이즈
대부분의 에어포일 생성기가 단위 코드길이를 기준으로 NACA Airfoil 수식에 따라 점들을 생성하고 이를 보간(Interpolation)한 커브를 사용하는데, 점의 좌표를 Airfoil Tools 사이트의 경우 소점 이하 6자리까지 수로 표현하고 있는데, 여기에서 실제 수식에 노이즈가 추가되는 현상이 발생합니다.
실제 아래 그림은 NACA 2412 형상을 Aifoil Tools 사이트에서 100개 점으로 생성하여 Degree=5의 커브로 Interpolation하여 그린 커브입니다. Trailing edge 부위의 곡률 그래프에서 볼 수 있듯이 곡률의 변화가 정상적이지 않은 것을 확인할 수 있는데, 이러한 현상이 소수점 6자리 이하 생략된 값에서 발생하는 것입니다.
**확대 그림에서는 곡률의 스케일을 더 키워 표시하였습니다.
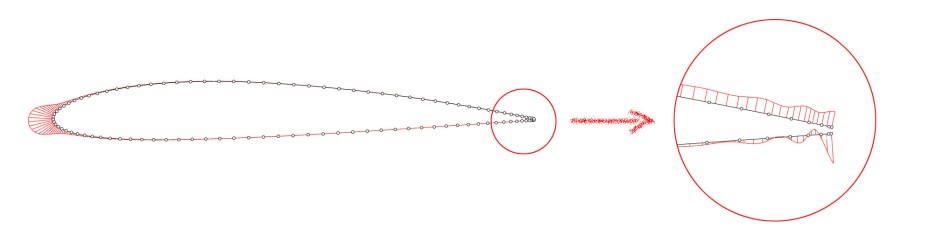
Aifoil Tools사이트의 NACA 2412 형상의 곡률 분포
문제점2. 획일적인 X좌표 간격
에어포일 형상의 특징 상 Leading Edge부분을 더 촘촘하게 점을 생성 시키고 비교적 곡
률이 작은 중 후반 부는 점 감격을 넓게 생성 시키는 것이 효과적인데, 많은 에어포일 생성기가
동일 간격(Linear)이나 사인파형(Sine, Cosine)에 의한 Leading, Trailing Edge 부분을 더 촘촘하게 하는 옵션만 있어 아쉬운 부분입니다.
Cosine, Linear Spacing
해결 방안. Grasshopper를 활용한 단면 생성
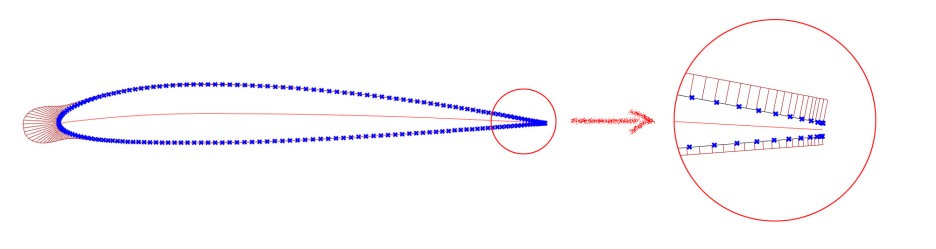
NACA단면을 Grasshopper에서 수식을 직접 계산하는 것만으로도 배정도(Double Precision) 로 수치 계산을 할 수 있어 소수점 단절에 의한 좌표점의 노이즈를 제거할 수 있습니다.
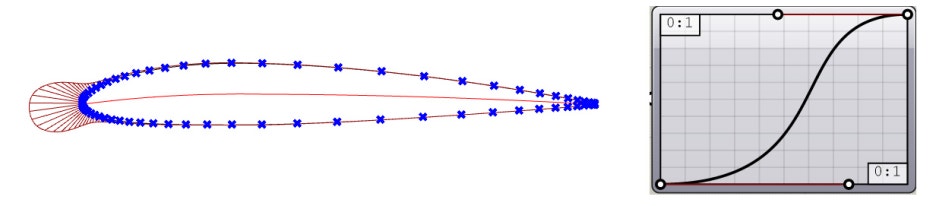
X좌표의 간격은 Grasshopper의 Graph Mapper를 이용하면 Sine, Linear외에도 Bezier를 이용하여 자유로운 밀도로 조절할 수 있어 편리하게 사용할 수 있습니다.
전송중...
Grasshopper로 생성한 NACA2312 곡선
전송중...
Graph mapper로 X좌표 밀도를 조절하여 점 개수를 50개로 줄인 형상
*수식 참조
NACA 4,5 자리 형상의 수식은 아래 페이지를 참조하였습니다.
https://en.wikipedia.org/wiki/NACA_airfoil
http://airfoiltools.com/airfoil/naca4digit
http://airfoiltools.com/airfoil/naca5digit
NACA 4 Digit Grasshopper Drawing
전송중...
사진 설명을 입력하세요.
**Python 코드
import math
a0 = 0.2969
a1 = -0.1260
a2 = -0.3516
a3 = 0.2843
xu=[];xl=[];yu=[];yl=[];cx=[];cy=[]
if ClosedTE :
a4 = -0.1036
else:
a4 = -0.1015
t = T/100
p = P/100
m = M/100
if T>=10:
tt = str(int(T))
else:
tt= "0"+str(int(T))
nacaStr = "NACA" + str(int(M)) + str(int(P/10)) + tt
for x in xx:
if x < p:
yc=(m/math.pow(p,2))*(2*p*x-math.pow(x,2))
dyc=(2*m/math.pow(p,2))*(p-x)
else:
yc=(m/math.pow((1-p),2))*(1-2*p+2*p*x-math.pow(x,2))
dyc=(2*m/math.pow((1-p),2))*(p-x)
theta = math.atan(dyc)
yt = 5*t * (a0*math.pow(x,0.5) + a1*x + a2*math.pow(x,2) + a3*math.pow(x,3) + a4*math.pow(x,4))
xu.append(chord*(x-yt*math.sin(theta)))
yu.append(chord*(yc+yt*math.cos(theta)))
xl.append(chord*(x+yt*math.sin(theta)))
yl.append(chord*(yc-yt*math.cos(theta)))
cx.append(chord*x)
cy.append(chord*yc)
NACA 5 Digit Grasshopper Drawing
전송중...
사진 설명을 입력하세요.
**Python 코드
import math
xu=[];xl=[];yu=[];yl=[];cx=[];cy=[]
a0 = 0.2969
a1 = -0.1260
a2 = -0.3516
a3 = 0.2843
if ClosedTE :
a4 = -0.1036
else:
a4 = -0.1015
L = int(naca[0])
PQ = naca[1:3]
Q = int(naca[2])
XX = int(naca[3:5])
clround = 3* L/20
clratio = clround/0.3
t = XX/100
if PQ=="10":
i=0
elif PQ=="20":
i=1
elif PQ=="30":
i=2
elif PQ=="40":
i=3
elif PQ=="50":
i=4
elif PQ=="21":
i=5
elif PQ=="31":
i=6
elif PQ=="41":
i=7
elif PQ=="51":
i=8
R = [0.058, 0.126, 0.2025, 0.29, 0.391, 0.13, 0.217, 0.318,0.441]
K1 = [361.4, 51.64, 15.957, 6.643, 3.23, 51.99, 15.793, 6.25, 3.191]
K2K1 = [0, 0, 0, 0, 0, 0.000764, 0.00677, 0.0303, 0.1355]
r = R[i]
k1 = K1[i]
k2k1 = K2K1[i]
for x in xx:
if Q==0 :
if (x
yc = clratio * ((k1/6)*(math.pow((x-r),3) - k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3) ))
dyc = clratio*((k1/6)*(3*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
else:
yc = clratio*((k1/6)*(k2k1*math.pow((x-r),3)-k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3)))
dyc= clratio*((k1/6)*(3*k2k1*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
else:
if (x < r):
yc = clratio*((k1/6)*((math.pow((x-r),3)-k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3))))
dyc = clratio*((k1/6)*(3*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
else:
yc = clratio*((k1/6)*(k2k1*math.pow((x-r),3)-k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3)))
dyc= clratio*((k1/6)*(3*k2k1*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
theta = math.atan(dyc)
yt=(t/0.2)*(a0*math.pow(x,0.5) + a1*x + a2*math.pow(x,2) + a3*math.pow(x,3) + a4*math.pow(x,4))
xu.append(chord*(x-yt*math.sin(theta)))
yu.append(chord*(yc+yt*math.cos(theta)))
xl.append(chord*(x+yt*math.sin(theta)))
yl.append(chord*(yc-yt*math.cos(theta)))
cx.append(chord*x)
cy.append(chord*yc)
**GH파일 다운로드

NACA 4, 5 Digit 에어포일...
대한민국 모임의 시작, 네이버 카페
cafe.naver.com
문제항공기 모델링에서 NACA Airfoil을 활용하는 경우가 많은데, Airfoil Tools http://airfoiltools.com/ 와 같은 웹 기반의 에어포일 생성기를 사용하는 경우를 많이 보게 됩니다.
문제점1. 좌표의 노이즈
대부분의 에어포일 생성기가 단위 코드길이를 기준으로 NACA Airfoil 수식에 따라 점들을 생성하고 이를 보간(Interpolation)한 커브를 사용하는데, 점의 좌표를 Airfoil Tools 사이트의 경우 소점 이하 6자리까지 수로 표현하고 있는데, 여기에서 실제 수식에 노이즈가 추가되는 현상이 발생합니다.
실제 아래 그림은 NACA 2412 형상을 Aifoil Tools 사이트에서 100개 점으로 생성하여 Degree=5의 커브로 Interpolation하여 그린 커브입니다. Trailing edge 부위의 곡률 그래프에서 볼 수 있듯이 곡률의 변화가 정상적이지 않은 것을 확인할 수 있는데, 이러한 현상이 소수점 6자리 이하 생략된 값에서 발생하는 것입니다.
**확대 그림에서는 곡률의 스케일을 더 키워 표시하였습니다.

Aifoil Tools사이트의 NACA 2412 형상의 곡률 분포
문제점2. 획일적인 X좌표 간격
에어포일 형상의 특징 상 Leading Edge부분을 더 촘촘하게 점을 생성 시키고 비교적 곡
률이 작은 중 후반 부는 점 감격을 넓게 생성 시키는 것이 효과적인데, 많은 에어포일 생성기가
동일 간격(Linear)이나 사인파형(Sine, Cosine)에 의한 Leading, Trailing Edge 부분을 더 촘촘하게 하는 옵션만 있어 아쉬운 부분입니다.
Cosine, Linear Spacing
해결 방안. Grasshopper를 활용한 단면 생성
NACA단면을 Grasshopper에서 수식을 직접 계산하는 것만으로도 배정도(Double Precision) 로 수치 계산을 할 수 있어 소수점 단절에 의한 좌표점의 노이즈를 제거할 수 있습니다.
X좌표의 간격은 Grasshopper의 Graph Mapper를 이용하면 Sine, Linear외에도 Bezier를 이용하여 자유로운 밀도로 조절할 수 있어 편리하게 사용할 수 있습니다.
Grasshopper로 생성한 NACA2312 곡선
Graph mapper로 X좌표 밀도를 조절하여 점 개수를 50개로 줄인 형상
*수식 참조
NACA 4,5 자리 형상의 수식은 아래 페이지를 참조하였습니다.
https://en.wikipedia.org/wiki/NACA_airfoil
http://airfoiltools.com/airfoil/naca4digit
http://airfoiltools.com/airfoil/naca5digit
NACA 4 Digit Grasshopper Drawing
사진 설명을 입력하세요.
**Python 코드
import math
a0 = 0.2969
a1 = -0.1260
a2 = -0.3516
a3 = 0.2843
xu=[];xl=[];yu=[];yl=[];cx=[];cy=[]
if ClosedTE :
a4 = -0.1036
else:
a4 = -0.1015
t = T/100
p = P/100
m = M/100
if T>=10:
tt = str(int(T))
else:
tt= "0"+str(int(T))
nacaStr = "NACA" + str(int(M)) + str(int(P/10)) + tt
for x in xx:
if x < p:
yc=(m/math.pow(p,2))*(2*p*x-math.pow(x,2))
dyc=(2*m/math.pow(p,2))*(p-x)
else:
yc=(m/math.pow((1-p),2))*(1-2*p+2*p*x-math.pow(x,2))
dyc=(2*m/math.pow((1-p),2))*(p-x)
theta = math.atan(dyc)
yt = 5*t * (a0*math.pow(x,0.5) + a1*x + a2*math.pow(x,2) + a3*math.pow(x,3) + a4*math.pow(x,4))
xu.append(chord*(x-yt*math.sin(theta)))
yu.append(chord*(yc+yt*math.cos(theta)))
xl.append(chord*(x+yt*math.sin(theta)))
yl.append(chord*(yc-yt*math.cos(theta)))
cx.append(chord*x)
cy.append(chord*yc)
NACA 5 Digit Grasshopper Drawing
사진 설명을 입력하세요.
**Python 코드
import math
xu=[];xl=[];yu=[];yl=[];cx=[];cy=[]
a0 = 0.2969
a1 = -0.1260
a2 = -0.3516
a3 = 0.2843
if ClosedTE :
a4 = -0.1036
else:
a4 = -0.1015
L = int(naca[0])
PQ = naca[1:3]
Q = int(naca[2])
XX = int(naca[3:5])
clround = 3* L/20
clratio = clround/0.3
t = XX/100
if PQ=="10":
i=0
elif PQ=="20":
i=1
elif PQ=="30":
i=2
elif PQ=="40":
i=3
elif PQ=="50":
i=4
elif PQ=="21":
i=5
elif PQ=="31":
i=6
elif PQ=="41":
i=7
elif PQ=="51":
i=8
R = [0.058, 0.126, 0.2025, 0.29, 0.391, 0.13, 0.217, 0.318,0.441]
K1 = [361.4, 51.64, 15.957, 6.643, 3.23, 51.99, 15.793, 6.25, 3.191]
K2K1 = [0, 0, 0, 0, 0, 0.000764, 0.00677, 0.0303, 0.1355]
r = R[i]
k1 = K1[i]
k2k1 = K2K1[i]
for x in xx:
if Q==0 :
if (x
yc = clratio * ((k1/6)*(math.pow((x-r),3) - k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3) ))
dyc = clratio*((k1/6)*(3*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
else:
yc = clratio*((k1/6)*(k2k1*math.pow((x-r),3)-k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3)))
dyc= clratio*((k1/6)*(3*k2k1*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
else:
if (x < r):
yc = clratio*((k1/6)*((math.pow((x-r),3)-k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3))))
dyc = clratio*((k1/6)*(3*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
else:
yc = clratio*((k1/6)*(k2k1*math.pow((x-r),3)-k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3)))
dyc= clratio*((k1/6)*(3*k2k1*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
theta = math.atan(dyc)
yt=(t/0.2)*(a0*math.pow(x,0.5) + a1*x + a2*math.pow(x,2) + a3*math.pow(x,3) + a4*math.pow(x,4))
xu.append(chord*(x-yt*math.sin(theta)))
yu.append(chord*(yc+yt*math.cos(theta)))
xl.append(chord*(x+yt*math.sin(theta)))
yl.append(chord*(yc-yt*math.cos(theta)))
cx.append(chord*x)
cy.append(chord*yc)
**GH파일 다운로드

NACA 4, 5 Digit 에어포일...
대한민국 모임의 시작, 네이버 카페
cafe.naver.com
항공기 모델링에서 NACA Airfoil을 활용하는 경우가 많은데, Airfoil Tools http://airfoiltools.com/ 와 같은 웹 기반의 에어포일 생성기를 사용하는 경우를 많이 보게 됩니다.
문제점1. 좌표의 노이즈
대부분의 에어포일 생성기가 단위 코드길이를 기준으로 NACA Airfoil 수식에 따라 점들을 생성하고 이를 보간(Interpolation)한 커브를 사용하는데, 점의 좌표를 Airfoil Tools 사이트의 경우 소점 이하 6자리까지 수로 표현하고 있는데, 여기에서 실제 수식에 노이즈가 추가되는 현상이 발생합니다.
실제 아래 그림은 NACA 2412 형상을 Aifoil Tools 사이트에서 100개 점으로 생성하여 Degree=5의 커브로 Interpolation하여 그린 커브입니다. Trailing edge 부위의 곡률 그래프에서 볼 수 있듯이 곡률의 변화가 정상적이지 않은 것을 확인할 수 있는데, 이러한 현상이 소수점 6자리 이하 생략된 값에서 발생하는 것입니다.
**확대 그림에서는 곡률의 스케일을 더 키워 표시하였습니다.
문제점2. 획일적인 X좌표 간격
에어포일 형상의 특징 상 Leading Edge부분을 더 촘촘하게 점을 생성 시키고 비교적 곡
률이 작은 중 후반 부는 점 감격을 넓게 생성 시키는 것이 효과적인데, 많은 에어포일 생성기가
동일 간격(Linear)이나 사인파형(Sine, Cosine)에 의한 Leading, Trailing Edge 부분을 더 촘촘하게 하는 옵션만 있어 아쉬운 부분입니다.
해결 방안. Grasshopper를 활용한 단면 생성
NACA단면을 Grasshopper에서 수식을 직접 계산하는 것만으로도 배정도(Double Precision) 로 수치 계산을 할 수 있어 소수점 단절에 의한 좌표점의 노이즈를 제거할 수 있습니다.
X좌표의 간격은 Grasshopper의 Graph Mapper를 이용하면 Sine, Linear외에도 Bezier를 이용하여 자유로운 밀도로 조절할 수 있어 편리하게 사용할 수 있습니다.
*수식 참조
NACA 4,5 자리 형상의 수식은 아래 페이지를 참조하였습니다.
NACA 4 Digit Grasshopper Drawing
**Python 코드
import math
a0 = 0.2969
a1 = -0.1260
a2 = -0.3516
a3 = 0.2843
xu=[];xl=[];yu=[];yl=[];cx=[];cy=[]
if ClosedTE :
a4 = -0.1036
else:
a4 = -0.1015
t = T/100
p = P/100
m = M/100
if T>=10:
tt = str(int(T))
else:
tt= "0"+str(int(T))
nacaStr = "NACA" + str(int(M)) + str(int(P/10)) + tt
for x in xx:
if x < p:
yc=(m/math.pow(p,2))*(2*p*x-math.pow(x,2))
dyc=(2*m/math.pow(p,2))*(p-x)
else:
yc=(m/math.pow((1-p),2))*(1-2*p+2*p*x-math.pow(x,2))
dyc=(2*m/math.pow((1-p),2))*(p-x)
theta = math.atan(dyc)
yt = 5*t * (a0*math.pow(x,0.5) + a1*x + a2*math.pow(x,2) + a3*math.pow(x,3) + a4*math.pow(x,4))
xu.append(chord*(x-yt*math.sin(theta)))
yu.append(chord*(yc+yt*math.cos(theta)))
xl.append(chord*(x+yt*math.sin(theta)))
yl.append(chord*(yc-yt*math.cos(theta)))
cx.append(chord*x)
cy.append(chord*yc)
NACA 5 Digit Grasshopper Drawing
**Python 코드
import math
xu=[];xl=[];yu=[];yl=[];cx=[];cy=[]
a0 = 0.2969
a1 = -0.1260
a2 = -0.3516
a3 = 0.2843
if ClosedTE :
a4 = -0.1036
else:
a4 = -0.1015
L = int(naca[0])
PQ = naca[1:3]
Q = int(naca[2])
XX = int(naca[3:5])
clround = 3* L/20
clratio = clround/0.3
t = XX/100
if PQ=="10":
i=0
elif PQ=="20":
i=1
elif PQ=="30":
i=2
elif PQ=="40":
i=3
elif PQ=="50":
i=4
elif PQ=="21":
i=5
elif PQ=="31":
i=6
elif PQ=="41":
i=7
elif PQ=="51":
i=8
R = [0.058, 0.126, 0.2025, 0.29, 0.391, 0.13, 0.217, 0.318,0.441]
K1 = [361.4, 51.64, 15.957, 6.643, 3.23, 51.99, 15.793, 6.25, 3.191]
K2K1 = [0, 0, 0, 0, 0, 0.000764, 0.00677, 0.0303, 0.1355]
r = R[i]
k1 = K1[i]
k2k1 = K2K1[i]
for x in xx:
if Q==0 :
if (x
yc = clratio * ((k1/6)*(math.pow((x-r),3) - k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3) ))
dyc = clratio*((k1/6)*(3*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
else:
yc = clratio*((k1/6)*(k2k1*math.pow((x-r),3)-k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3)))
dyc= clratio*((k1/6)*(3*k2k1*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
else:
if (x < r):
yc = clratio*((k1/6)*((math.pow((x-r),3)-k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3))))
dyc = clratio*((k1/6)*(3*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
else:
yc = clratio*((k1/6)*(k2k1*math.pow((x-r),3)-k2k1*math.pow((1-r),3)*x-math.pow(r,3)*x+math.pow(r,3)))
dyc= clratio*((k1/6)*(3*k2k1*math.pow((x-r),2)-k2k1*math.pow((1-r),3)-math.pow(r,3)))
theta = math.atan(dyc)
yt=(t/0.2)*(a0*math.pow(x,0.5) + a1*x + a2*math.pow(x,2) + a3*math.pow(x,3) + a4*math.pow(x,4))
xu.append(chord*(x-yt*math.sin(theta)))
yu.append(chord*(yc+yt*math.cos(theta)))
xl.append(chord*(x+yt*math.sin(theta)))
yl.append(chord*(yc-yt*math.cos(theta)))
cx.append(chord*x)
cy.append(chord*yc)
**GH파일 다운로드






1 comment:
Great read thankss
Post a Comment